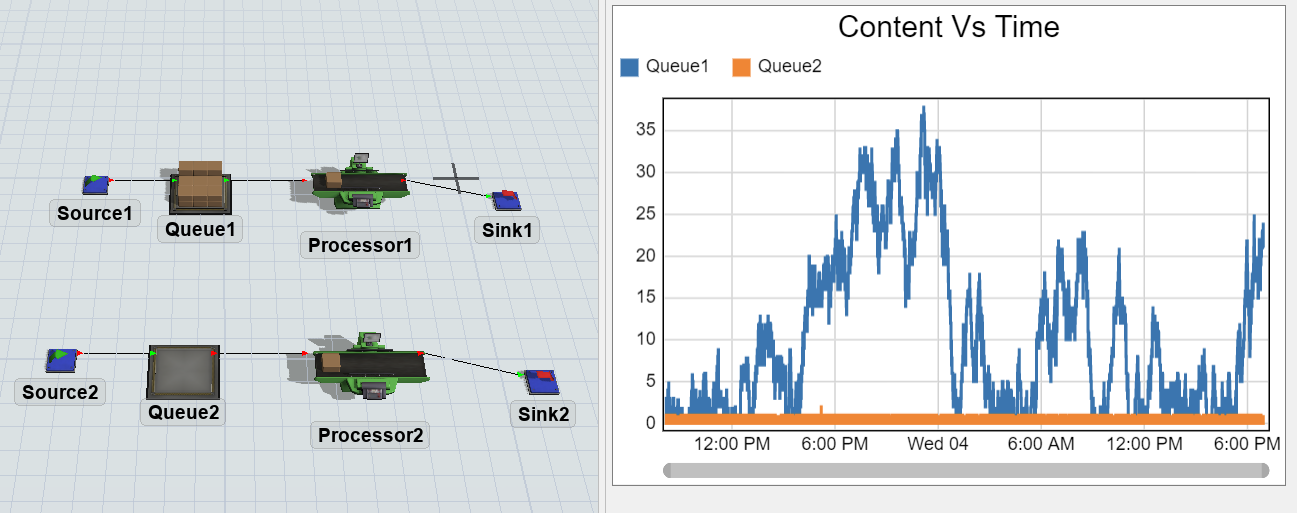
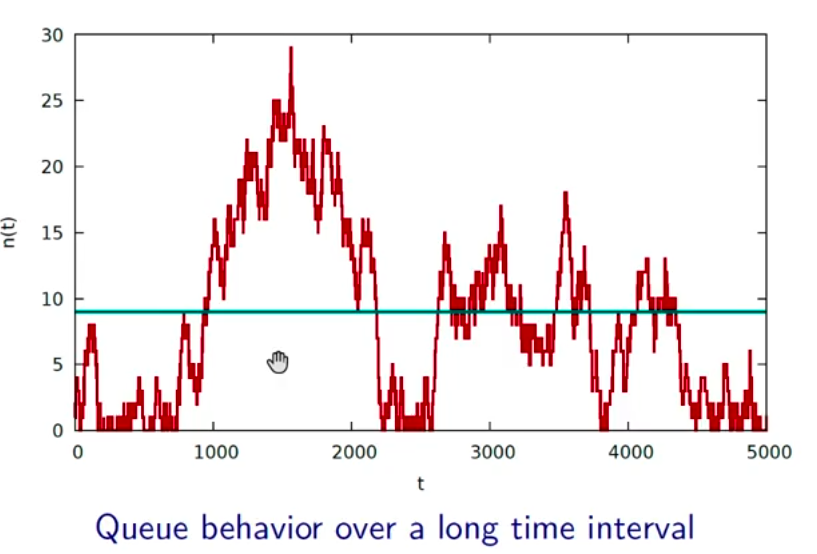
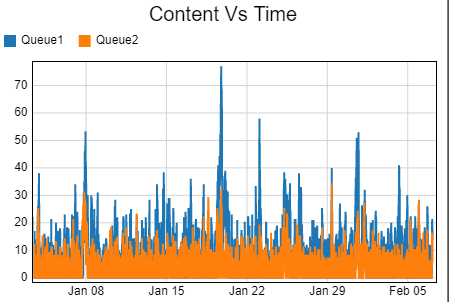
in a simple M/M/1 system with identical parameters of poisson arrival time and processing time but different units, getting different results for the average content in the queue
1) arrival time = 1 min, processing time =0.9 minute
2) arrival time = 60 sec, processing time = 54 sec
Please post a model. This is difficult to investigate from just the screenshot and the description.
according to the exact formula the average parts in the queue is (54/60)/(1-(54/60)) = 9 parts
After looking at this model, I think FlexSim is performing the calculations as expected. The issue is misusing the Poisson distribution.
Here's what happens. Processor 1 uses poisson(0.9) to calculate how long items need to process. If you just sample the poisson(0.9) distribution 10 times, here is a set of answers you could get:
[0, 1, 3, 0, 1, 0, 0, 3, 0, 1]
FlexSim then converts these values from minutes into model units, so you get something like this:
[0, 60, 180, 0, 60, 0, 0, 180, 0, 60]
Processor 2, on the other hand, uses poisson(54). Sampling that distribution 10 times gives values like these:
[60, 47, 55, 51, 49, 50, 56, 63, 63, 62]
You can see that these values are very, very different from the first set of values. This is why the first processor takes so much longer than the second.
I say it's a misuse of the Poisson distribution because when you sample the Poisson distribution, you get a result of "how many events" not "how long between events".
However, if you use something like the Date Time Source, you can specify how many arrivals you would like each time period. That would be a very good place to use the Poisson distribution.
but still can't see why the second process doesn't behave as expected or near the formula.
The processing time difference isn't actually a big contributor to gap in the results. With the same arrival data the two queues have this content:
But you're also misusing the poisson as the interarrival time on the source objects - one being set to minutes and the other seconds.
If you think your arrivals are following a Poisson process then the interarrival times should be using negative exponential distribution - again not poisson.
14 People are following this question.
FlexSim can help you understand and improve any system or process. Transform your existing data into accurate predictions.
FlexSim is a fully 3D simulation software environment. FlexSim can be used to simulate any process in any industry.
FlexSim®, FlexSim Healthcare™, Problem Solved.®, the FlexSim logo, the FlexSim X-mark, and the FlexSim Healthcare logo with stylized Caduceus mark are trademarks of FlexSim Software Products, Inc. All rights reserved.
