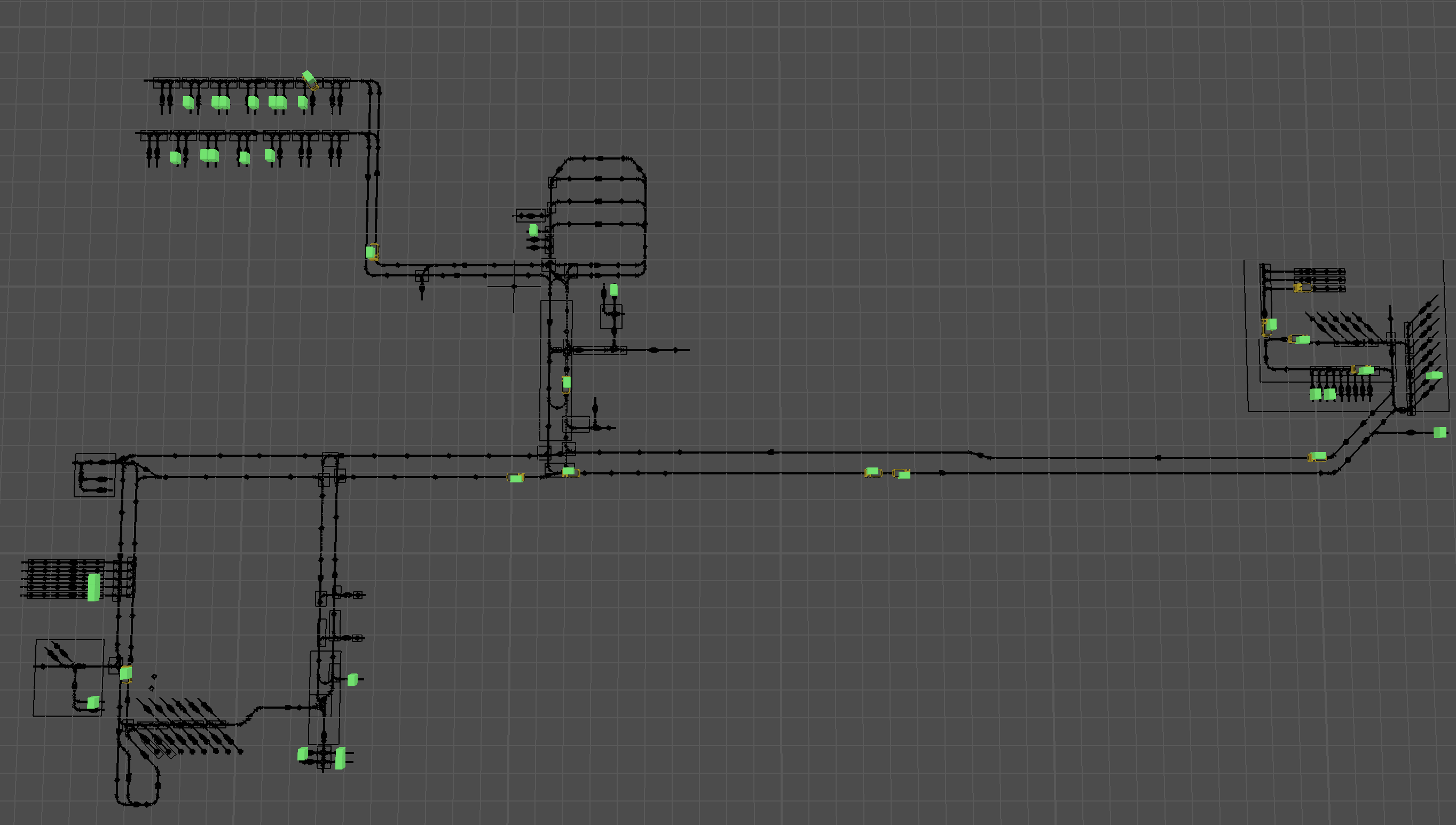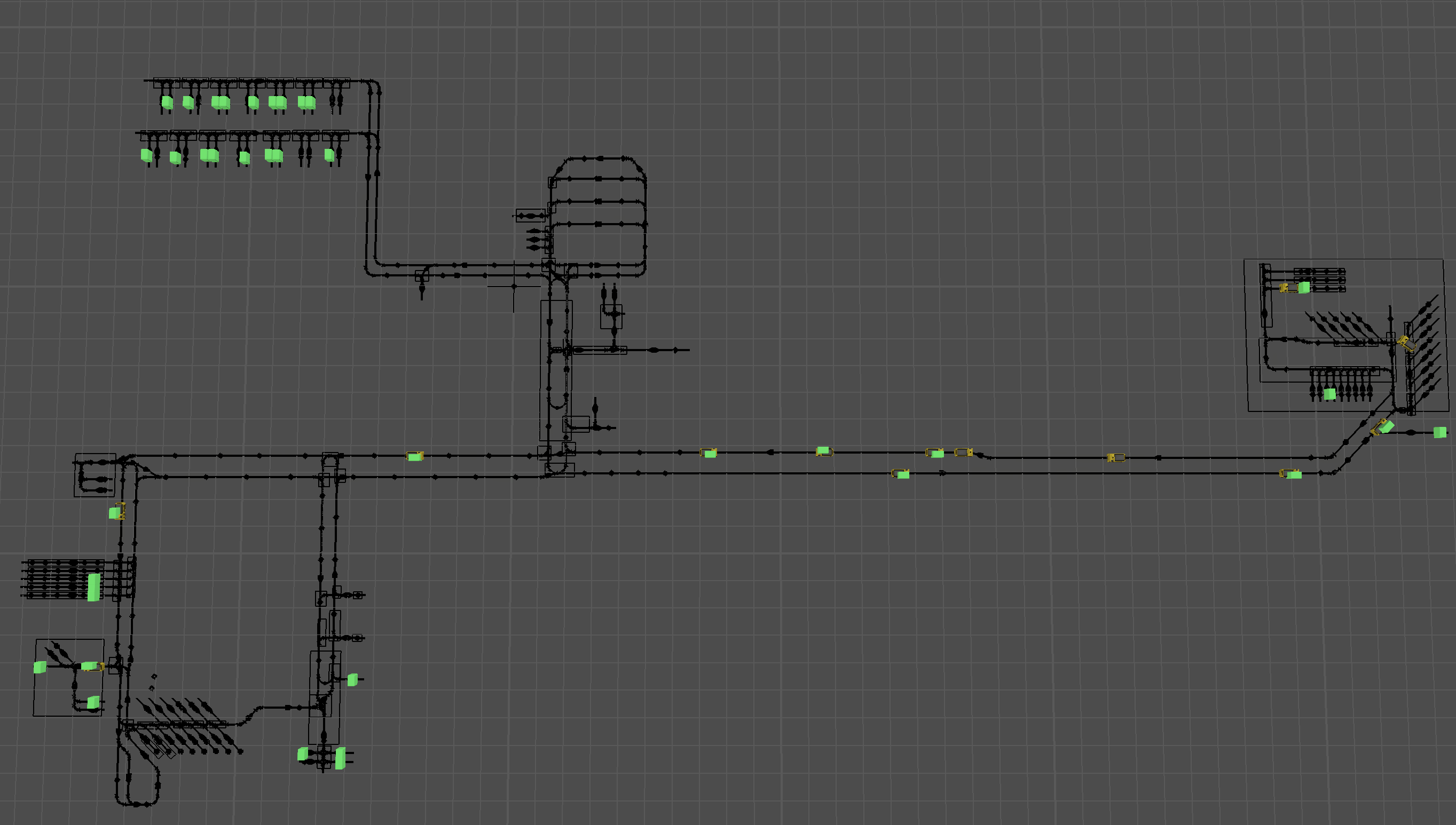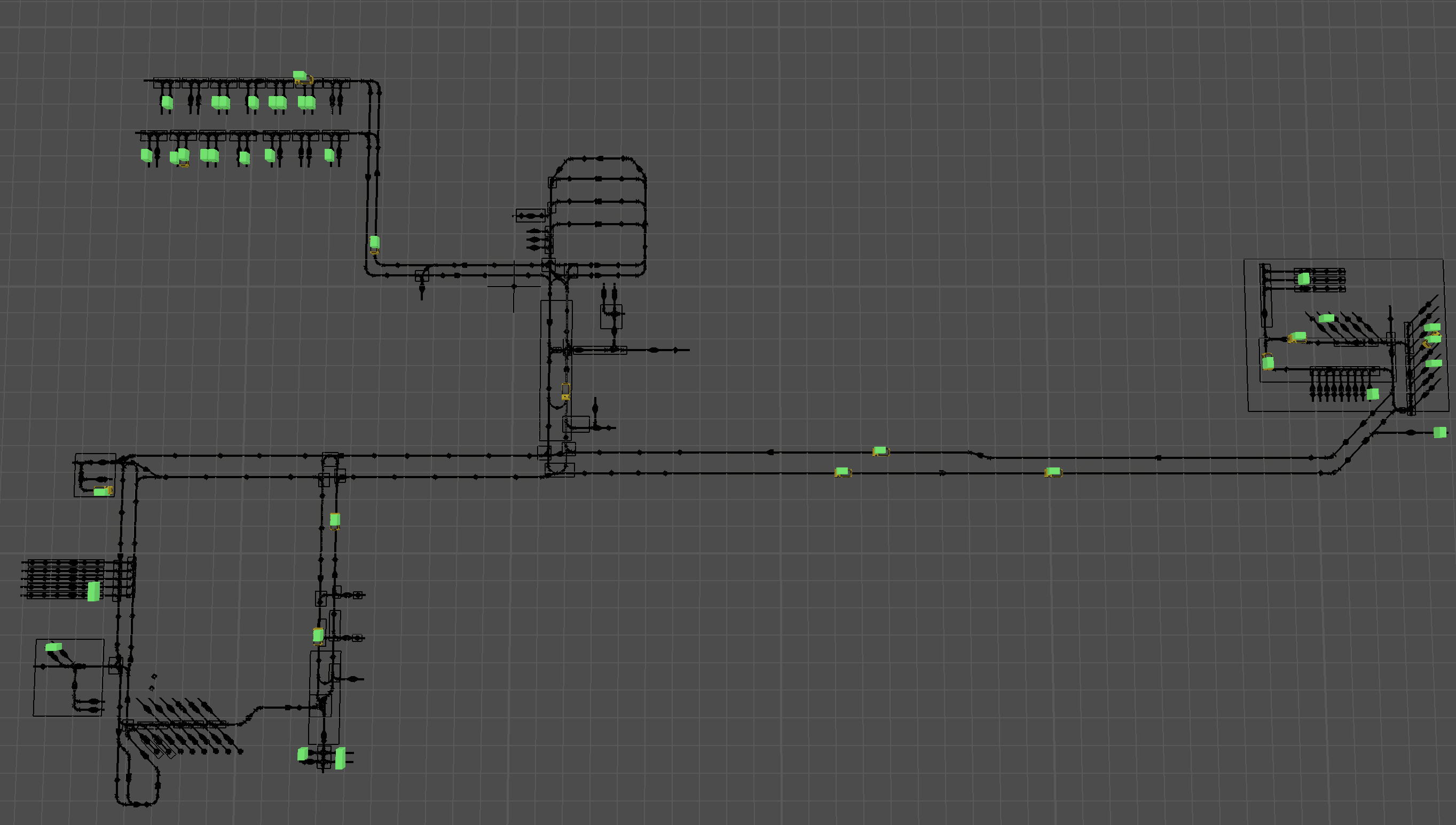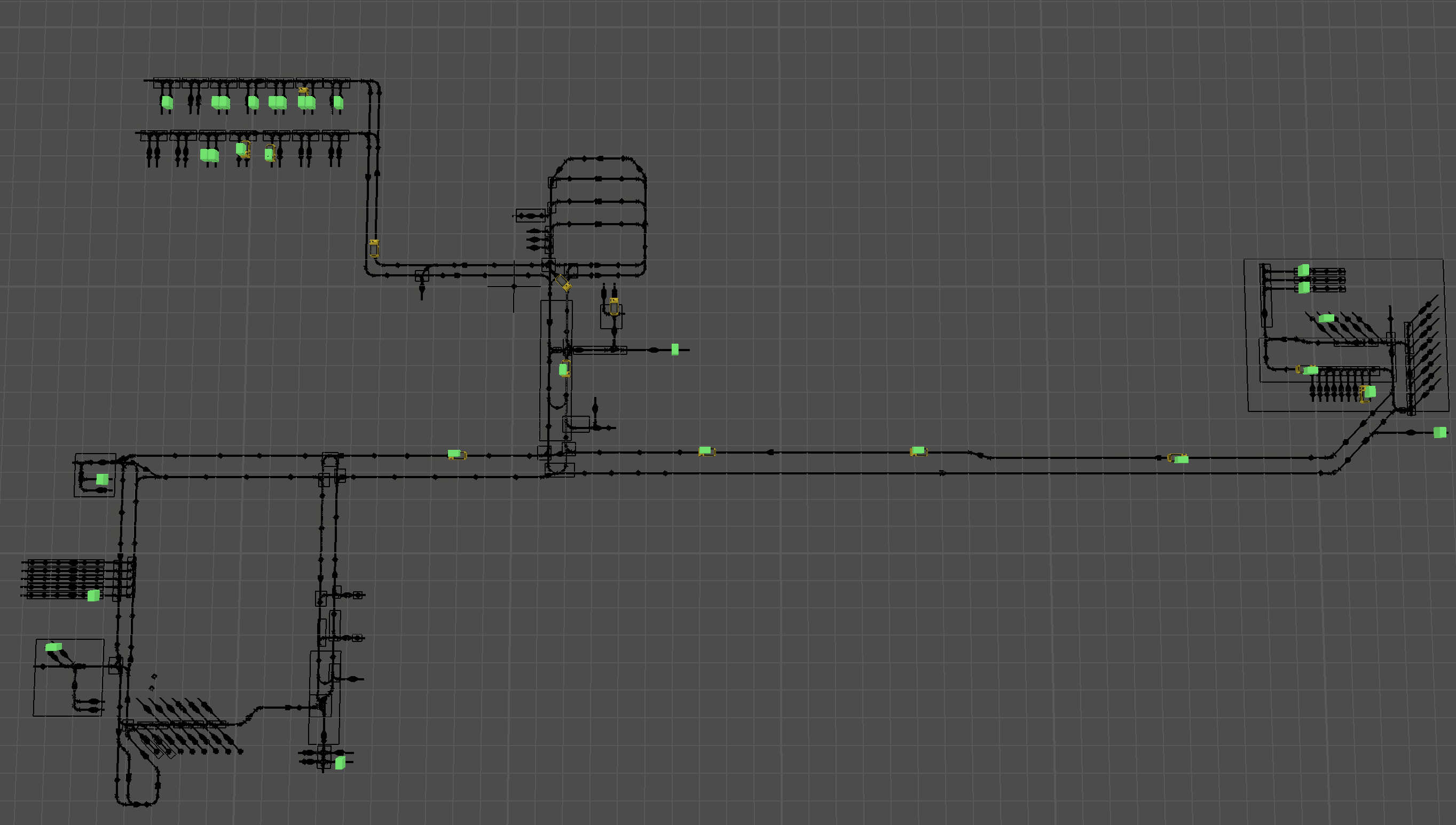
 Attached is a sample model that uses Google's OR-Tools python module to find optimal AGV dispatching solutions.
Attached is a sample model that uses Google's OR-Tools python module to find optimal AGV dispatching solutions.
I recently stumbled on Google's OR-Tools, which includes several classes for finding optimal solutions to things like vehicle routing, scheduling, bin packing, etc. Since FlexSim now has a mechanism for easy connection to python, I decided to try and see if/how it could be connected to FlexSim for testing AGV dispatching strategies. I threw together this model just to see how/if the connection can work. All source/destination locations are chosen at random, and work inter-arrival rates are random with a user-defined mean inter-arrival time.
To get this model running on your side:
- Install a version of python
- Run the following from the command-line: python -m pip install ortools
- In FlexSim, make sure your preferences are configured for the correct version of python, and that python is part of your PATH environment variable.
- Open the model.
- In the Parameters table, set DispatchMode to 'VRP Solver'.
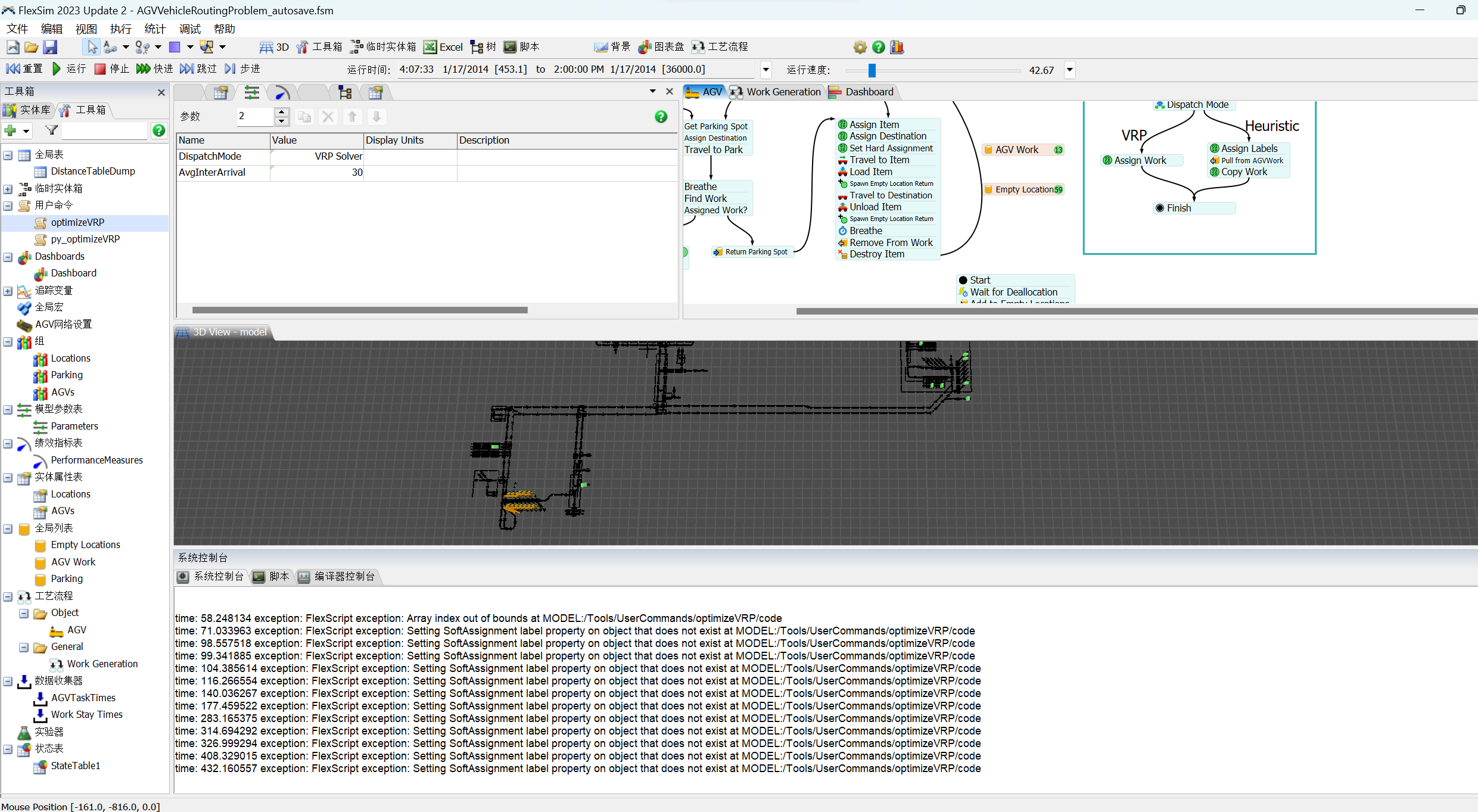
This model uses the Vehicle Routing Problem solver to find optimal AGV assignment strategies. The main work generation logic is in the 'Work Generation' process flow. At random intervals, work requests arrive. They are assigned to random source and destination locations. Then, when dispatching in 'VRP Solver' mode, the logic calls the optimizeVRP() user command. This command packages the current state of the model into a valid vehicle routing problem, and then passes it to the py_optimizeVRP() user command, which is implemented in python, in the AGVVRP.py file. The command creates the VRP problem using the OR-Tools classes, and then calls the solver, returning the results. OptimizeVRP() then interprets the results and assigns AGVs as needed. Note that the VRP is re-solved every time new work arrives. You'll see little 'freezes' in the execution of the model, because it is solving the VRP at each work arrival.
Note that the standard Vehicle Routing Problem is slightly different from the problem this model needs optimized:
- In an AGV model, there’s no depot. Instead AGVs may be currently located anywhere in the warehouse.
- There’s no ‘depot-loaded’ capacity of an AGV, and no ‘demand’ at customers. The standard VRP is a situation where trucks are loaded at the depot, and then depleted as they visit each customer in the route. This is not present with single-capacity AGVs.
- When an AGV picks up at an origin location, it must immediately deliver to the destination location.
In order to wrangle the AGV problem into a valid vehicle routing problem that can be solved by OR-Tools, I constructed the problem as follows:
- I made each AGV’s ‘current location’ a node in the graph
- The distance from the depot to the AGV’s current location is 0
- The distance from the depot to any other node in the graph is prohibitively large. This will cause vehicles to always go to their 'current location' first, with 0 cost.
- The distance from any node in the graph back to the depot is 0
- A given AGV must visit its current location as part of its route. This can be added as a constraint to the problem in OR-Tools
- For immediate unload after loading, I initially tried adding this rule as a constraint, but the solver hung when solving. So, instead of graph nodes being locations in the facility, I made graph nodes represent ‘tasks’, i.e. visiting this node means picking up the item AND dropping it off.
- As such, the ‘cost’ of ‘visiting’ a ‘task’ node is the cost to travel from the ‘destination’ of the previous node to the ‘origin’ of this ‘task’ node, plus the cost to travel from the ‘origin’ of this task node to the destination of this ‘task’ node.
Once I did this, OR-Tools was able to solve the problem 'optimally'. By optimally, I mean it was finding the AGV routing that minimized the maximum 'travel makespan', which is the maximum distance route of all of the AGVs.
Once I had done this, I wanted to compared it with various heuristic-based scenarios. So I set up a 'Closest' dispatch mode. Here, when an AGV finishes a task, it will take up the next task whose pickup point is closest to its current position. I also created a 'FIFO' dispatching mode, which is that work will be dispatched to AGVs always in FIFO order. These three dispatching modes I compared with the experimenter.
My initial experiments showed some interesting results. Most interesting was that in 'VRP Solver' mode, work task time-in-system was relatively high. This is because the objective function completely ignored time in system of the work, and was only optimizing for vehicle travel distance. So some work was being pushed off until much later because vehicles could get better travel distances by pushing it off. To account for this, I added a 'soft upper bound', which is kind of like a 'due date' for the work. Namely, work is due to be finished 800 'meters-of-agv-travel' after it arrives. This was a quick-and-dirty workaround and could certainly be improved, but it did serve to get the time in system for VRP Solver mode down.
Below are some of the resulting experimenter results.
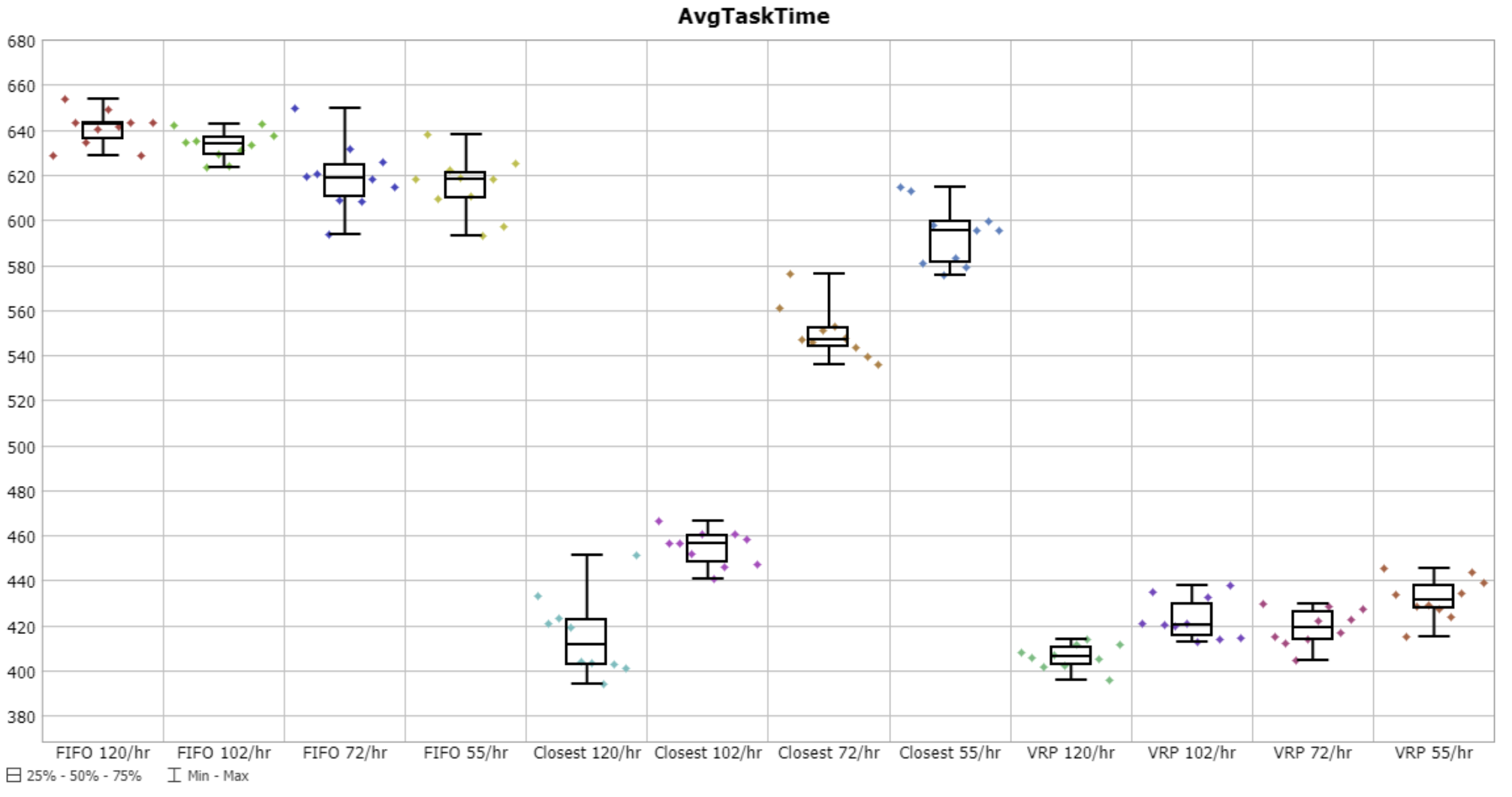
AGVTaskTime - Time from starting a task to finishing it (i.e. a kind of takt time)
The VRP solver performed the best across all scenarios here, and was especially better than the other strategies in low-demand scenarios. This intuitively makes sense. When there are a lot of under-utilized AGVs, the closest and FIFO strategies will always dispatch idle AGVs to do work, which could potentially make them travel long distances. However, the VRP solver can find opportunities to decrease travel distance by waiting to dispatch an AGV that will be near a task in the future, and leave other AGVs idle.
Note that I think the 'closest' strategy only finds the 'closest' next task for an AGV that just finished a task, not the 'closest' idle AGV for an arriving task. Obviously that could be changed for a better performing 'closest' strategy. On the other hand, I think in this model all idle AGVs go back to the same park location, so such a change would require distributed park locations to take advantage of closer idle AGVs.
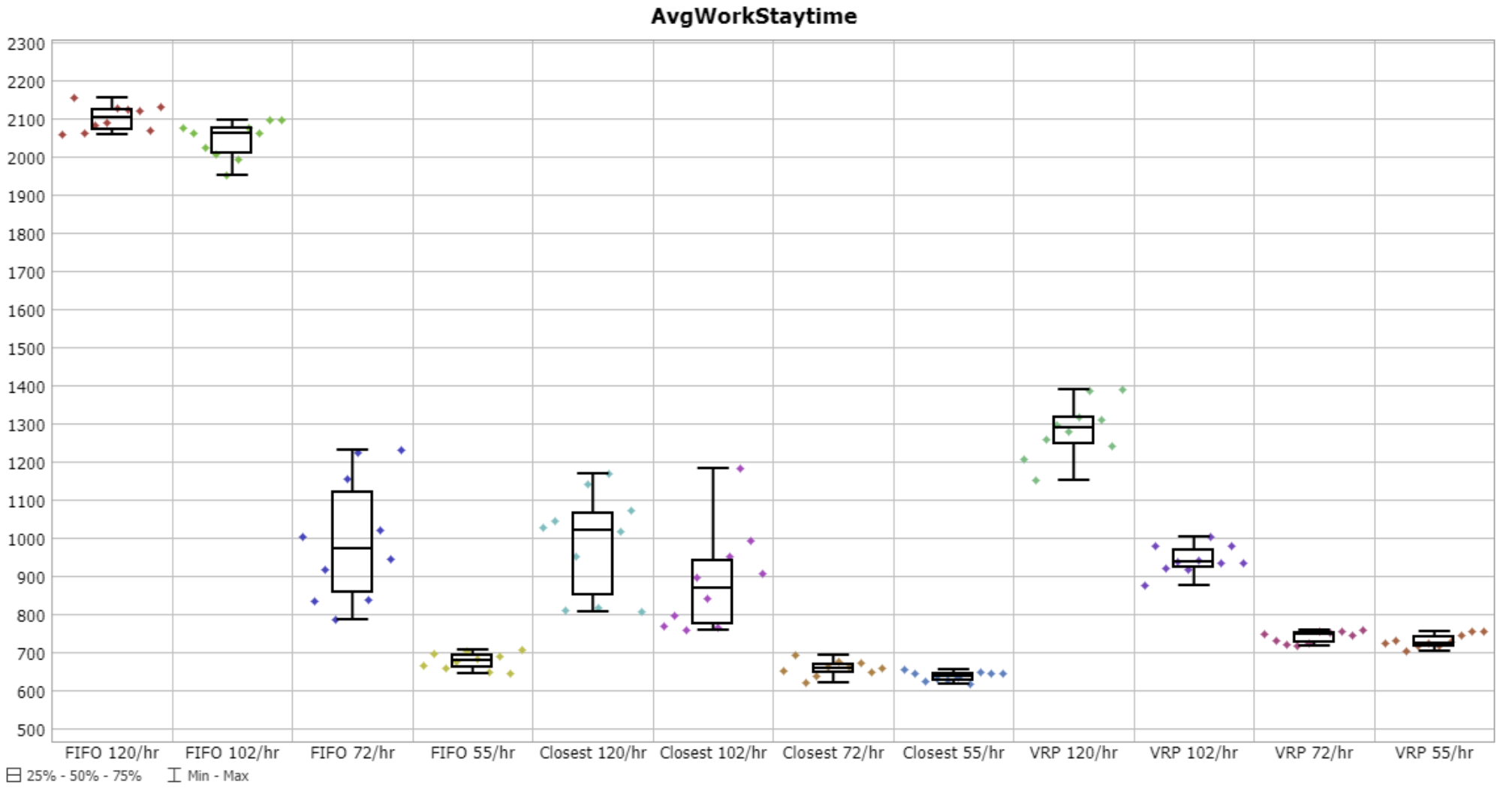
AGVWorkStaytime - time-in-system for a given AGV task
Here the 'closest' strategy actually performed better than the VRP. This would seem counter-intuitive at first, but upon further evaluation, it does make sense. The VRP, in its current form, only optimizes for total AGV travel distance. It completely ignores job time in system/due dates/etc. So the solver will always assign a route that is shorter even if that route pushes back jobs that have been in the queue for a long time. The solver also re-solves every time a new job arrives. So we may be having scenarios where some jobs are always 'better' to be pushed to the end of the route, and so they keep getting pushed back, resulting in poor time-in-system performance.
The solver does include soft and hard job 'due dates', so we could make adjustments to the problem to make the VRP get better time-in-system results.
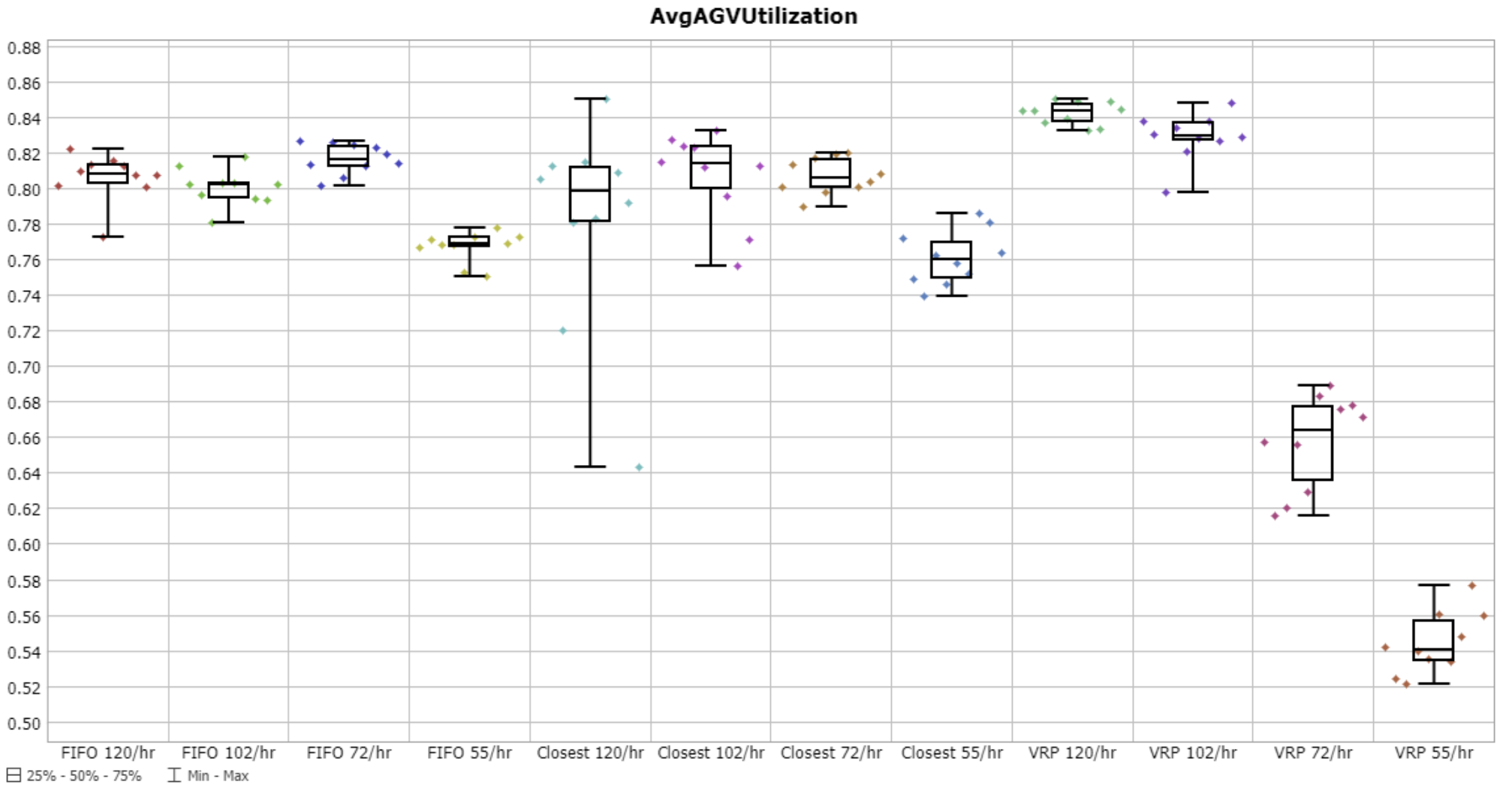
AvgAGVUtilization
AvgAGVUtilization is where the VRP especially shines in low-demand scenarios. It finds opportunities to leave AGVs parked because there will be opportunities for busy AGVs to take up jobs in the future with minimal extra travel overhead, whereas the 'FIFO' and 'Closest' strategies will always dispatch idle AGVs to unassigned jobs, causing extra unnecessary empty travel.
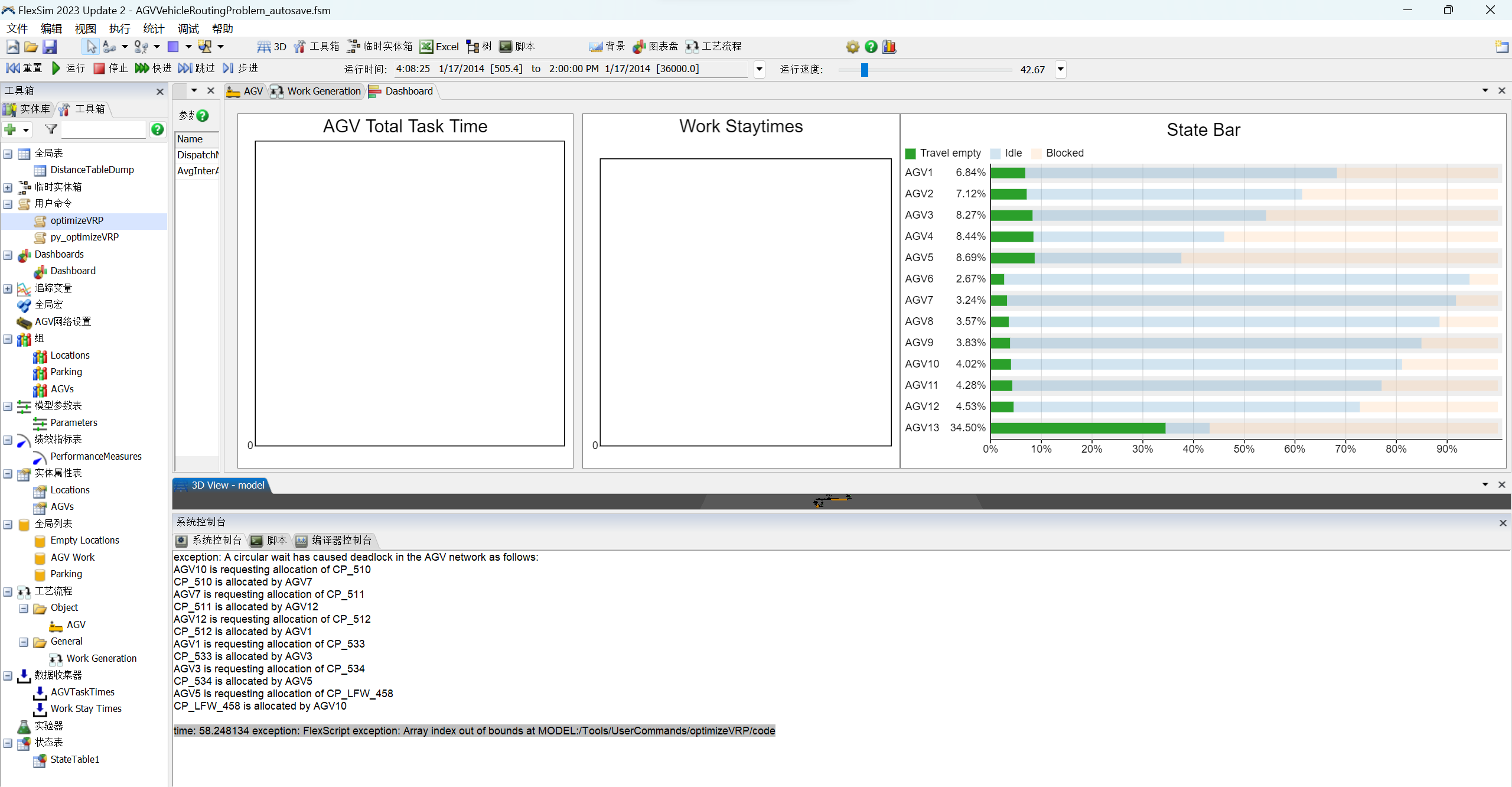
I am still a bit perplexed by the high-demand scenarios though. Here the 'Closest' and 'FIFO' strategies both beat the VRP in the 120/hr and 102/hr scenarios. This probably would warrant further investigation as to why the other strategies do better here. It may be that, in these scenarios, the AGVs cannot keep up with demand. So there is a queue of jobs that is ever-increasing. The VRP solver is optimizing the full plan, meaning it is scheduling job assignments, and finding travel distance minimization opportunities, that are way out into the future. And it is not getting the opportunity to execute those optimized routes because the problem is being re-solved at each job arrival. With an increasing job queue, the 'closest' and 'fifo' strategies might be actually doing better specifically because they are short-sighted. Just take the closest job to you. On the other hand, if we have increasing job queues (i.e. the AGVs can't keep up), then the AGV utilization should be around 100% anyway, which it's not. Anyway, it's something still to churn on.
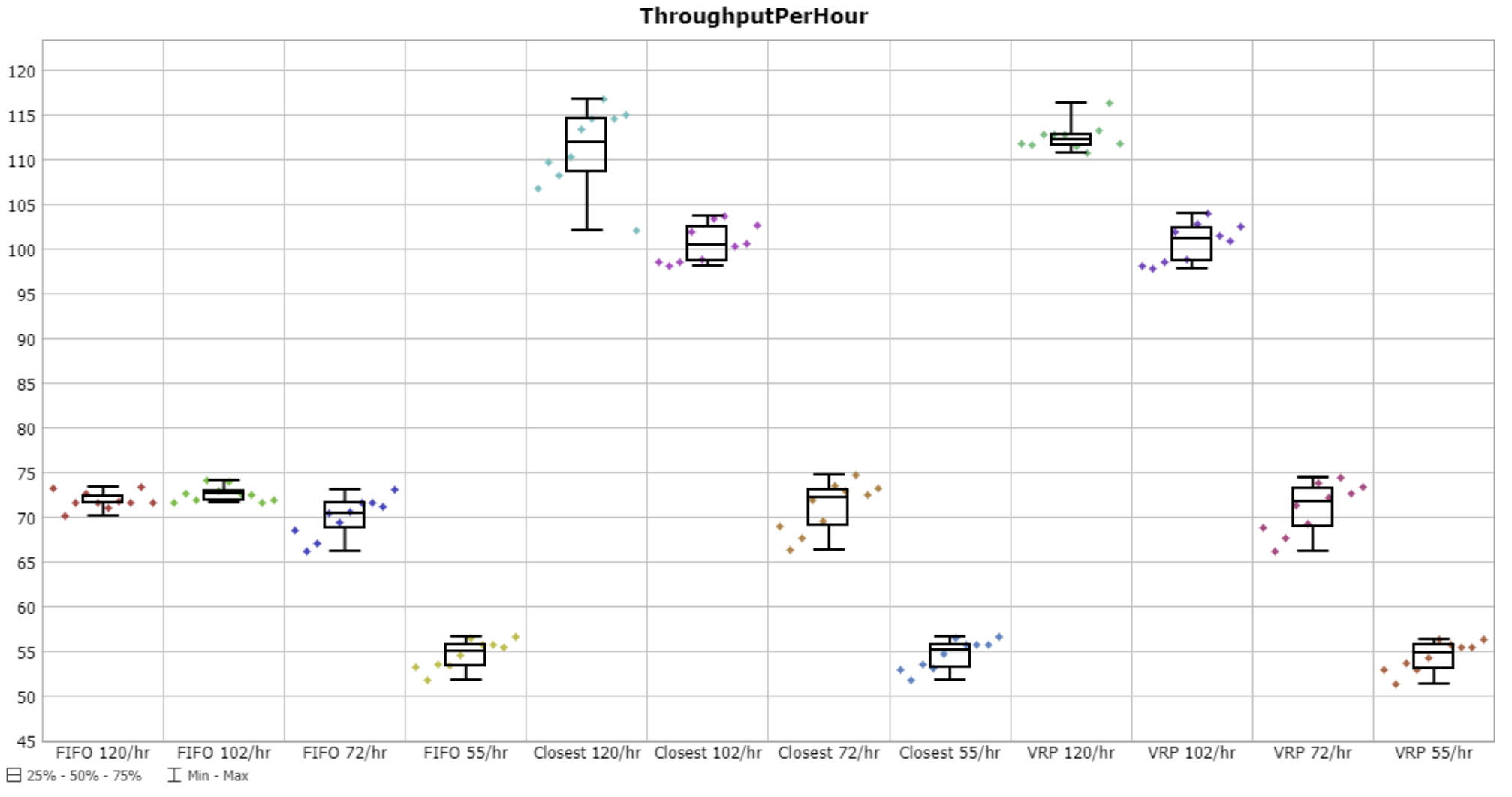
ThroughputPerHour
The throughput per hour indicator tells us whether the AGVs actually kept up with the jobs. If the AGVs were able to keep up with jobs, then the resulting means should be right around the scenario's throughput/hr number. It looks like FIFO got way behind on both the 120/hr and 102/hr scenarios. 'Closest' and VRP both got a little behind in the 120/hr scenarios.
One exciting possibility of using this design is that the python script is not technically dependent on FlexSim. So you can use FlexSim to test your python-based optimization, and then you can deploy that python script in a live setting.